Thread
Do neural networks learn 'universal' solutions or idiosyncratic ones? We find inherent randomness. Models consistently learn group composition via an interpretable, representation theory (!) based algorithm. Yet they even skip simple reps for complex ones! arxiv.org/abs/2302.03025
In collaboration with @NeelNanda5 and @justanotherlaw, we build on their prior work reverse-engineering grokking in modular addition (i.e. cyclic group composition). Their trig-based algorithm generalises via rep theory to arbitrary group composition, and many results transfer.
We leverage this understanding of networks performing group composition to build a toy model of universality. Universality asserts networks learn canonical solutions and motifs as opposed to arbitrary ad-hoc ones, so insights from interpreting one model may carry over to others!
Preliminary work by @ch402 found distinct vision models tend to learn similar, universal, components: curve and high-low frequency detector neurons. If we can understand enough such components we may be able to understand network behaviour in general. distill.pub/2020/circuits/zoom-in/
What even is rep theory? Groups are fundamentally about symmetries. Rep theory thinks of a group as symmetries of a vector space, so elements are linear maps! S5 is about permuting 5 points, and our model thinks of it as linear maps permuting the 5 corners of a 4D tetrahedron.
The representation theoretic algorithm for group composition we find at a high level uses rep theory to map group elements to representation matrices, multiply these matrices, and then converts back to group elements.
Each group has a finite set of fundamental irreducible representations. Each gives a separate (often qualitatively different) implementation of our algorithm. This offers an excellent algorithmic test bed for 'universality'! Empirically, all of them are used in some situations.
This algorithm directly generalises what @NeelNanda5 found for modular addition of p elements - i.e. composition on the cyclic group of order p. Representations are 2x2 rotation matrices, with each frequency a different irreducible representation.
Recently, mech interp has shifted to finding small, toy models a more tractable setting to develop insights relevant to interpreting the practical or SOTA models we really care about. If universality holds, these insights will carry over to real models and this is useful.
But if not, the mech interp community may be wasting substantial effort, and should shift focus to developing scalable, more automated interpretability techniques directly capable of interpreting models of genuine interest. So, understanding universality better is important!
To study universality we train ~100 networks of two different architectures on composition of various groups. We bootstrap our initial understanding of one network (see later) to automate the reverse engineering of many more. We find mixed evidence for universality.
We find compelling evidence for what we call WEAK universality. ALL networks learn our algorithm. Our algorithm defines a family of features (reps) and circuits for all groups - we find this characterises completely the set of circuits learned by networks on this task.
To us, the algorithm initially seems unnecessarily complex, but it turns out networks may implement it easily by abusing linearity. This illustrates the inductive biases of networks differ massively from our inductive biases.
Translating a symbolic problem into linear algebra seems like a robustly useful approach for a neural network (a linear algebra machine) to take and perhaps could be WHY this algorithm is so universal across groups and architectures.
We however find evidence against STRONG universality. Each group has several representations that could be learned, all offering valid solutions to the problem. Under the strongest form of universality, networks should consistently learn the SAME features and circuits.
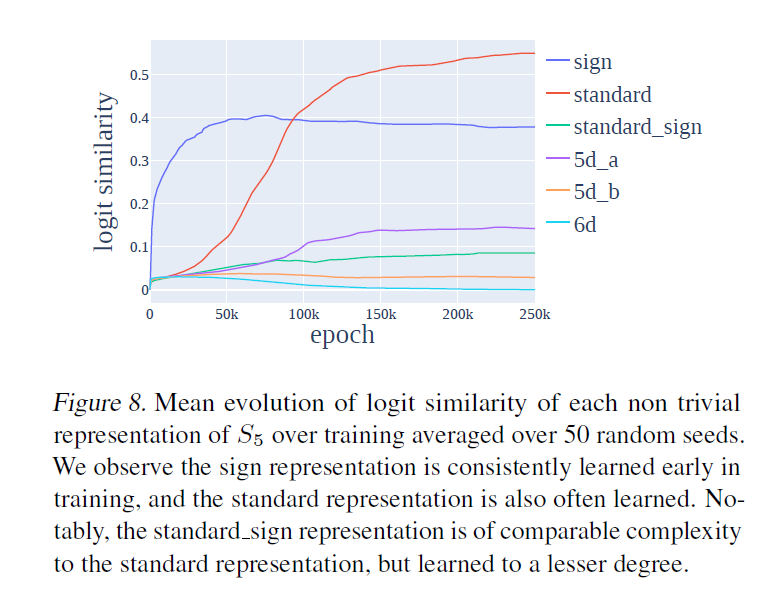
But, we find for a fixed group, the SPECIFIC representations, and NUMBER of representations learned vary wildly across random seed, and network architecture. While not deterministic, lower dimensional features tend to be learned more often than higher - a probabilistic trend?
We did not expect this! We thought networks would prefer some reps (and associated features and circuits) over others, and deterministically learn those, given the algorithm for different reps offers differing performance, and the reps themselves are of varying complexity.
We do find lower dimensional reps are generally (but not always) learned earlier during training. The sign (parity) representation is obviously the simplest rep (1x1 matrices containing 1 bit of information), and is always learned first. The subsequent trend is less clear.
What are the implications of this work for mechanistic interpretability? Interpreting a particular behaviour on a single network seems insufficient for fully understanding that behaviour in general on arbitrary networks on simple algorithmic tasks, let alone real networks.
By studying MANY models it may be possible to uncover a 'periodic table' of universal circuits, like our algorithm over all possible reps, that if all understood give full understanding of behaviour, and from which networks may choose arbitrarily during training.
Further, the lottery ticket hypothesis (@jefrankle) asserts this choice may even be encoded and understandable at initialization. @NeelNanda5 found weak evidence for this in at least one group. Checking whether this is the case for arbitrary groups feels an exciting extension!
How do we actually know our networks implement this algorithm? We present a detailed analysis on one network trained on composition of S_5:
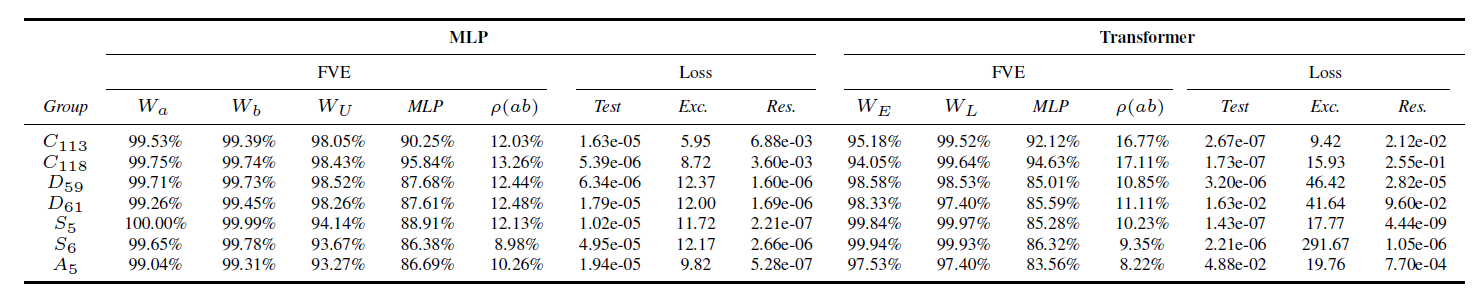
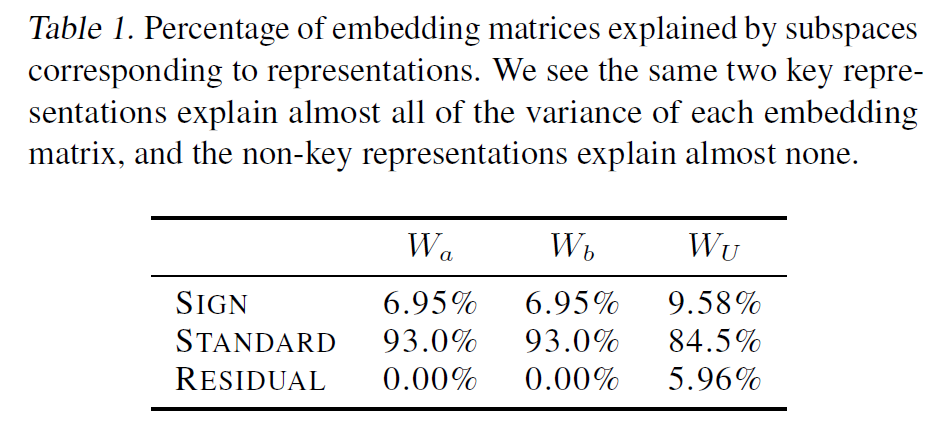
1) Logit Attribution. Our algorithm predicts the form of logits. By computing the correlation of these logits with the true logits with we find the model learns 2 of the possible 6 reps: 'sign' and 'standard', which we call 'key reps', explaining 85% of logits in 2 directions!
2) Our algorithm predicts the embeddings and unembeddings to be memorised look up tables of the representation matrices in required by the algorithm. We can just read off that it's learned these, AND the reps learned, which agree with (1).
3) MLP neurons are used to multiply the matrices corresponding to a and b, giving the matrix corresponding to ab in the key reps. We validate this by just reading off this term from the neuron activations!
Once the neurons have computed the product ab, we can just read off how this is mapped to the output logits, and it's exactly what our algorithm says!
4) Ablations. If we remove everything BUT our algorithm, performance improves! Removing any piece from our algorithm majorly damages performance.
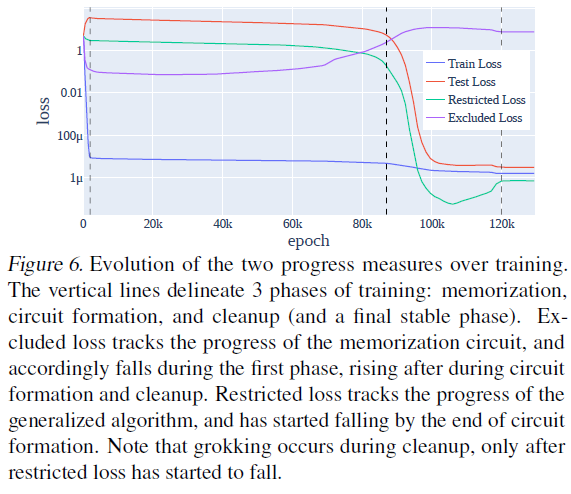
Though mech interp is often labour intensive, we often find deep and generalisable insights from it. @NeelNanda5 found a seemingly ad-hoc algorithm for modular addition, which we show has a deep generalisation to any group - we are too able to replicate their results on grokking.
Grokking is sudden generalisation much later in training after initial overfitting. @NeelNanda5's results via progress measures instantly generalise to arbitrary groups, explaining grokking on S5 originally found by @exteriorpower.
Thanks again to my co-authors, @justanotherlaw for assisting in the framing and distilling of results and editing assistance, and to @NeelNanda5 for mentoring and proposing the project!
For more on reverse engineering, universality, as well as other bonus content (including more on rep theory, inductive biases, double grokking and pretty visualisations) check out our paper (also my first!) on arxiv: arxiv.org/abs/2302.03025
In this work we build heavily on prior work on reverse engineering networks performing modular addition by @NeelNanda5, @justanotherlaw, @lieberum_t, Jess Smith, and @JacobSteinhardt (arxiv.org/abs/2301.05217).
Our approach of circuits style mechanistic interpretability is heavily inspired by work pioneered by @ch402, @nickcammarata @catherineols, @nelhage, @trishume, and others.
Mentions
There are no mentions of this content so far.